How Math Symbols Influence Math Performance

Authors: Sarah Powell and Melissa Driver

To perform most math calculations, students use numerals (e.g., 4, 29, ¾) and symbols (e.g., +, >, ÷). Numerals and symbols are often referred to as “symbolic” or “abstract” representations of mathematics (Bruner, 1966; Miller & Hudson, 2006). In this brief, we refer to such representations as “symbolic.” It is important that students know how to solve symbolic math problems because classroom assignments and high-stakes assessments almost exclusively use symbolic representations to test student’s math knowledge.

     To investigate how symbolic representations affect math performance, we, along with our research team, conducted two randomized-control trials with second-grade students. In the first, we asked students to practice addition with different types of equations (i.e., standard and nonstandard) to see how students could learn the relational definition of the equal sign. In the second, we worked on addition in symbolic and nonsymbolic (i.e., without numerals and symbols) forms to determine which approach was better for learning addition. See Figure 1 for an example of contrasting symbolic and nonsymbolic forms.

Figure 1. Symbolic and Nonsymbolic Examples

Study #1: Standard and Nonstandard Equations

In previous work about one critical math symbol, the equal sign (=), we learned that students often misinterpret the equal sign as a signal to do something when the equal sign should be interpreted as “the same as” or “balance” (Powell & Fuchs, 2010). This is problematic considering the equal sign is present in equations students solve in both elementary and secondary math. One common hypothesis about the reason that students interpret the equal sign incorrectly is that students only see and work with standard (e.g., 3 + 5 = __; 9 – __ = 2) equations in elementary school classrooms (McNeil, 2008). Elementary math curricula rarely, if ever, present nonstandard (e.g., 2 + 4 = __ + 3; 6 = 10 – __) equations to students (Powell, 2012). See Figure 2 for examples of standard and nonstandard equations. With both types of equations, students should try to make the two sides on either side of the equal sign the same. With standard equations, students often do not have to interpret the equal sign as relational (i.e., two side of an equations are the same, or balanced). Students can solve standard equations by interpreting the equal sign as operational. Our study examined whether students could learn to interpret the equal sign as relational if presented with a combination of standard and nonstandard equations.

Figure 2. Examples of Standard and Nonstandard Equations

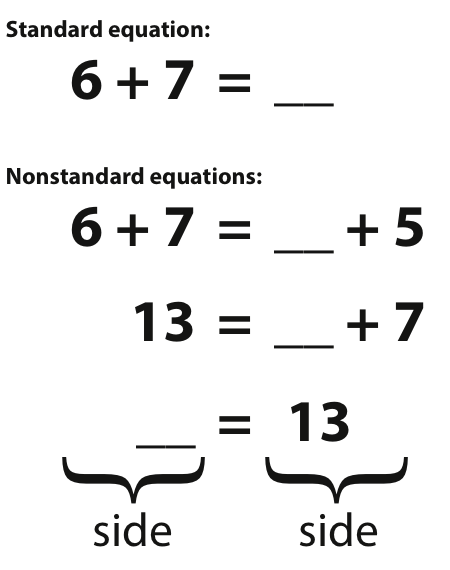
Second-grade students who performed below the 10^th percentile on a test of single-digit addition facts were recruited as participants. We identified 51 students out of 524, and the 51 students were randomly assigned to (a) addition tutoring with standard equations only, (b) addition tutoring with standard and nonstandard equations, or (c) no-tutoring control. Students in the two active tutoring groups received 15 sessions of individual tutoring over a period of 5 weeks. Each tutoring session lasted approximately 10-12 minutes. Tutoring sessions focused on helping students understand the concept of addition, and provided practice with solving addition problems. Students in the standard group only worked on addition presented in the standard format (e.g., 2 + __ = 6; 1 + 7 = __), whereas students in the standard and nonstandard group worked on addition presented in standard and nonstandard formats (e.g., 5 = 2 + __; 4 + 2 = __ + 1; 9 + __ = 11; __ = 6). See Figure 3 for a comparison of student worksheets. During the first tutoring session, the tutors talked with students in both groups about interpreting the equal sign as “the same as.” During subsequent tutoring sessions, tutors discussed the concept of balancing the two sides of the equation. The equation format (i.e., standard vs. standard/nonstandard) was the only difference between the two tutoring groups.

Figure 3. Standard Worksheet (S) Compared to Standard/Nonstandard Worksheet (N)

Based on posttest data, with pretest as a covariate, the students in the combined-equation group (i.e., standard and nonstandard equation practice) outperformed students in the standard-equations-only and no-tutoring groups on tests of equation solving and equal-sign understanding (Powell, Driver, & Julian, in press). As we provided little explicit equal-sign instruction in both tutoring groups, we concluded that the exposure to and practice solving a combination of standard and nonstandard equations proved helpful in improving students’ ability to interpret the equal sign in a relational manner.

Study #2: Symbolic and Nonsymbolic Representations

     In our second study, we investigated whether addition performance differed when problems were presented in symbolic and nonsymbolic form. We developed our hypothesis out of prior assessment work where students were able to solve nonstandard equations with blocks and plates, but the same students had difficulty with solving the same nonstandard equations in symbolic form (Sherman & Bisanz, 2009). For example, when students were presented with four plates (two plates on one side of the table and two plates on the other side, with three of the plates containing a number of blocks) and asked to make the sides the same, about ¾ of students completed this task correctly. On the other hand, fewer than 40% of students could solve the corresponding symbolic equation (e.g., __ + 4 = 6 + 3) correctly. See Figure 4 for an example of this task where the student has to place circle counters in the empty box to make the two sides (of the black stick) the same.

Figure 4. Nonstandard Equations Task With Manipulatives

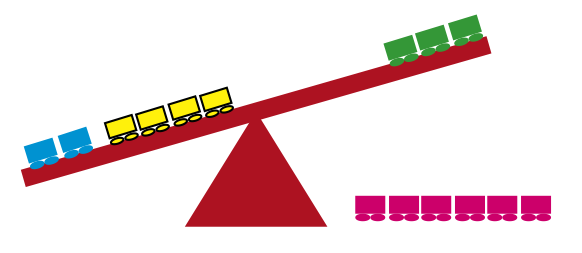
     Similar to Study #1, second-grade students who performed below the 10^th percentile on a test of single-digit addition facts were recruited as participants. We identified 55 students (out of 574) and randomly assigned students to (a) addition tutoring in symbolic form, (b) addition tutoring in symbolic and nonsymbolic forms, and (c) no-tutoring control. Tutors tutored students for 12 sessions, and each session lasted approximately 10-12 minutes. The addition equations in both tutoring groups were exactly the same. In the symbolic-only group, students learned the concept of addition and practiced with numbers and symbols on paper as well as numbers and symbols they could touch and manipulate (i.e., magnetic numbers and symbols). In the symbolic and nonsymbolic group, students practiced the concept of addition with a balance and cubes, clips, motor manipulatives, and pictures of dogs and cats, as well as with numbers and symbols. See Figure 5 for an example with a balance and manipulative trains. We thought about only using nonsymbolic forms to practice addition, but as all tests measure addition knowledge through symbolic representation, we presented students with the combination of symbolic and nonsymbolic representations.

Figure 5. Using a Balance Scale to Solve the Equation 2 + 4 = __ + 3

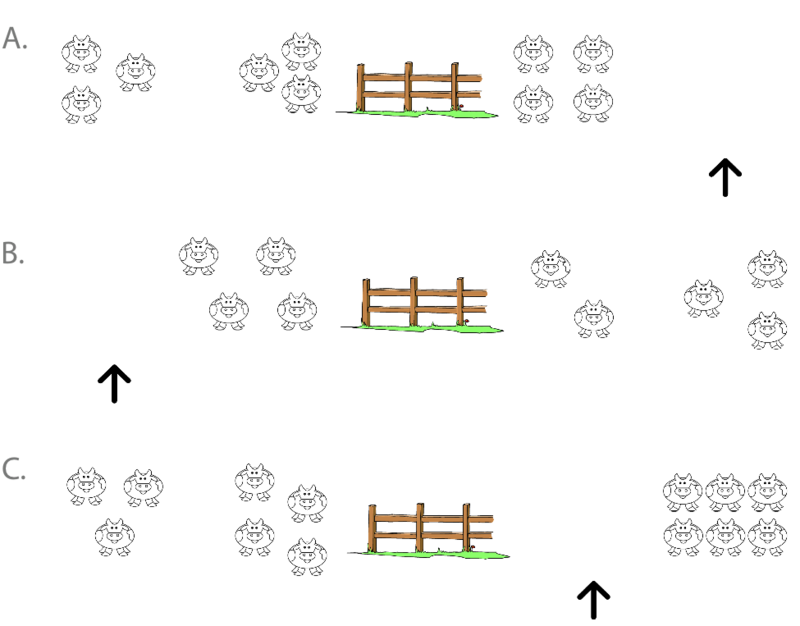
We are currently working on the data analysis of Study #2. The length of tutoring within our study was fairly brief, so we would like to replicate this project with another group of students, providing at least 18 to 24 tutoring sessions. Interestingly, we administered a test of nonstandard equations in symbolic format (e.g., 2 + 3 = __ + 1) and nonsymbolic format (e.g., **  *** (line) ___ *) to all 574 students, and the results confirm the hypothesis that students perform better on nonsymbolic items over symbolic items (Driver & Powell, 2013). See Figure 6 for an example of the nonsymbolic task where students had to draw cows (above the arrow) to help a farmer place the same number of cows on each side the fence. Students with and without mathematics difficulties could solve the nonsymbolic pictorial representations with approximately 83% accuracy. Students solved symbolic representation with less than 40% accuracy. The preliminary data from the tutoring study suggest that students in the combination group of symbolic and nonsymbolic tutoring demonstrated slight significant gains over the students in the symbolic-only tutoring group. The results from this project indicate that students are more successful with math problems presented without numerals and symbols, yet we need to do more investigation on the effect a combination symbolic and nonsymbolic tutoring package can have for students with math difficulties.

Figure 6. Nonsymbolic, Nonstandard Equations

Future Research on Math Symbols

     Our final project related to math symbols investigated the effect of explicit vocabulary instruction on the meaning of math symbols (e.g., plus, minus, equals) and other math words used to explain addition (e.g., together, more, less, add). We provided tutoring to first-grade students with math difficulty. Half of the tutoring students received explicit vocabulary instruction on addition, and the other half did not. We have not conducted data analysis on this third project, but we hope to learn whether explicit vocabulary instruction is a necessary component of math tutoring. If it is, we hope to extend the vocabulary tutoring to include symbols related to subtraction, comparing numbers, multiplication, and division.

      So, are math symbols important? Yes. Students need to use numerals and symbols to solve almost every math problem in school. Do math symbols affect performance? Yes. In our first study, we learned that students interpret the equal sign differently based on their practice with different types of equations. In our second study, we learned that students can solve the same problem, presented in different ways, and that students perform better on problems without numerals and symbols.

Applying This to the Classroom

      Although our work in the area of math symbols is new and emerging, we feel it is important for classroom teachers to understand several things. First, we cannot assume students understand math symbols. The term “plus sign” is commonly used, but do students know what it means? If students relate the symbol to “adding,” can they explain what it means to “add?” It is imperative that teachers provide explicit instruction and practice on identifying and interpreting symbols. Even more so than at the elementary level, teachers of students in older grades assume students understand mathematical symbols. We feel instruction on symbols should occur at the elementary, middle, and high school levels. Second, teachers should provide students with novel ways to understand symbols. Teaching using nonstandard equations may help students understand the equal sign relationally. This, in turn, may help students with their algebraic reasoning (Kieran, 1991; Molina, Castro, & Ambrose, 2005). The use of nonsymbolic forms of addition may also help students demonstrate math understanding and learning before students can demonstrate the same knowledge in symbolic form.

References

Bruner, J. S. (1966). Toward a theory of instruction. Cambridge, MA: Belkapp Press.

Driver, M. K., & Powell, S. R. (2013). The influence of symbols in mathematics problem solving: Student performance on tasks of equivalence. Manuscript submitted for publication.

Kieran, C. (1991). Helping make the transition to algebra. The Arithmetic Teacher, 38(7), 49-51.

McNeil, N. M. (2008). Limitations to teaching children 2 + 2 = 4: Typical arithmetic problems can hinder learning of mathematics equivalence. Child Development, 79,1524-1537. http://dx.doi.org/10.1111/j.1467-8624.2008.01203.x

Miller, S. P., & Hudson, P. J. (2006). Helping students with disabilities understand what mathematics means. Teaching Exceptional Children, 39(1), 28-35.

Molina, M., Castro, E., & Ambrose, R. (2005). Enriching arithmetic learning by promoting relational thinking. International Journal of Learning, 12, 265-270.

Powell, S. R. (2012). Equations and the equal sign in elementary mathematics textbooks. Elementary School Journal, 112, 627-648. http://dx.doi.org/10.1086/665009

Powell, S. R., Driver, M. K., & Julian, T. E. (in press). The effect of tutoring with nonstandard equations on the mathematics performance of second-grade students with mathematics difficulty. Journal of Learning Disabilities.

Powell, S. R., & Fuchs, L. S. (2010). Contribution of equal-sign instruction beyond word-problem tutoring for third-grade students with mathematics difficulty. Journal of Educational Psychology, 102, 381-394. http://dx.doi.org/10.1037/a0018447

Sherman, J., & Bisanz, J. (2009). Equivalence in symbolic and nonsymbolic contexts: Benefits of solving problems with manipulatives. Journal of Educational Psychology, 101, 88-100. http://dx.doi.org/10.1037/a0013156